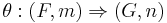Monoidal natural transformation
Suppose that 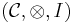 and
and 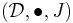 are two monoidal categories and
are two monoidal categories and
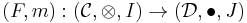 and
and 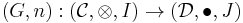
are two lax monoidal functors between those categories.
A monoidal natural transformation
between those functors is a natural transformation 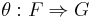 between the underlying functors such that the diagrams
between the underlying functors such that the diagrams
- and
commute for every objects  and
and  of
of 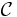 .
.
A symmetric monoidal natural transformation is a monoidal natural transformation between symmetric monoidal functors.